Question

A 0.58 kg mass is moving horizontally with a speed of 6.0 m/s when it strikes a vertical wall. The mass rebounds with a speed of 4.0 m/s. What is the magnitude of the change in linear momentum of the mass

Answer 1

`5.8\; {\rm kg\cdot m \cdot s^(-1)}`.

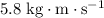Step-by-step explanation:

If the mass of an object is
`m` and the velocity of that object is
`v`, the linear momentum of that object would be
`m\, v`.

Assume that the initial velocity of the mass is positive (
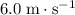`6.0\; {\rm m\cdot s^(-1)}`.) However, the direction of the velocity is reversed after the impact. Thus, the sign of the new velocity of the object would be negative- the opposite of that of the initial velocity. The new velocity would be
`(-4.0\; {\rm m\cdot s^(-1)})`.

Thus, the change in the velocity of the mass would be:

`\begin{aligned}& (\text{Change in Velocity}) \\ =\; & (\text{Final Velocity}) - (\text{Initial Velocity}) \\ =\; & (-4.0\; {\rm m\cdot s^(-1)}) - (6.0\; {\rm m\cdot s^(-1)}) \\ =\; & (-10\; {\rm m\cdot s^(-1))\end{aligned}`.

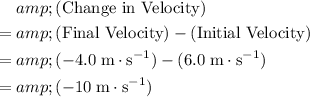The change in the linear momentum of the mass would be:

`\begin{aligned} & \text{change in momentum} \\ =\; & (\text{mass}) * (\text{change in velocity}) \\ =\; & 0.58\; {\rm kg} * (-10\; {\rm m\cdot s^(-1)}) \\ =\; & (-5.8\; {\rm kg \cdot m \cdot s^(-1)})\end{aligned}`.

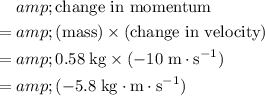Thus, the magnitude of the change of the linear momentum would be
`5.8\; {\rm kg \cdot m \cdot s^(-1)}`.