Question

Carmen is going to rent a truck for one day. There are two companies she can choose from, and they have the following prices.Company A charges $129 and allows unlimited mileage.Company B has an initial fee of $75 and charges an additional $0.90 for every mile driven.For what mileages will Company A charge less than Company B?Use m for the number of miles driven, and solve your inequality for m.

Answer 1

For a mileage greater than 60 miles.

Step-by-step explanation

Let the number of miles be m.

Company A charges $129 while company B has an initial fee of $75 and charges an additional $0.90 for every mile driven.

We have to write an expression for the charges of Company B:

`75+0.90m`

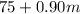
For the charges of company A to be less than company B, it implies that:

`129<75+0.90m`

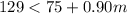
Solve from m in the inequality above:

`\begin{gathered} 129-75<0.90m \\ \Rightarrow0.90m>54 \\ (0.90m)/(0.90)>(54)/(0.90) \\ \Rightarrow m>60 \end{gathered}`

Therefore, the cost of Company A will be less than Company B when the mileage is more than 60 miles.