Given:
a.) Hans runs 6 miles in 45 minutes.
To be able to determine how many minutes would he take to run 4 miles, we will be using ratio and proportions.
We get,
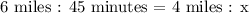
Where,
x = time he would take to run 4 miles.
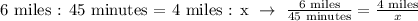
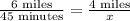
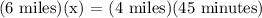
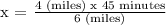
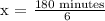
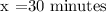
Therefore, it'll take 30 minutes for Hans to run 4 miles.