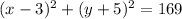Question

Write the standard form equation of a circle that passes through (8,7) with the center (3,-5)

Answer 1

The standard equation of a circle is given by:

`(x-h)^2+(y-k)^2=r^2`

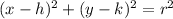
Where r is the radius and the center is located at (h, k).

Since the center is at (3, -5), we have h = 3 and k = -5.

Now, to calculate the radius, let's use the point (8, 7) in the equation and solve it for r:

`\begin{gathered} (8-3)^2+(7-(-5))^2=r^2\\ \\ 5^2+12^2=r^2\\ \\ r^2=25+144\\ \\ r^2=169\\ \\ r=13 \end{gathered}`

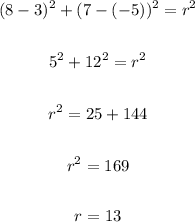
Therefore the equation of the circle is:

`(x-3)^2+(y+5)^2=169`