Question

Two cyclists start at the same point and travel in opposite directions. One cyclist travels 4 km/h slower than the other. If the two cyclists are 216 kilometers apart after 4 hours, what is the rate of each cyclist?

Answer 1

Let the rate of the faster cyclist be x km/h. Now, this means the rate of the slower cyclist, who is 4 km/h slower than the other is: (x - 4) km/h

Since the two cyclists are travelling opposite each other, we have that:

`(rate\text{ of faster cyclist + rate of slower cyclist)}* time\text{ = their distance apart}`

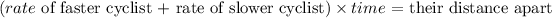
Since we have that the two cyclist are said to be at a distance of 216 km apart after a time of 4 hours, we have that:

`\begin{gathered} (rate\text{ of faster cyclist + rate of slower cyclist)}* time\text{ = their distance apart} \\ \Rightarrow(x+(x-4))*4=216 \end{gathered}`

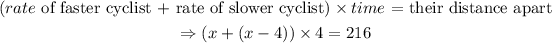
Now, we have to solve the resulting equation for the value of x, as follows:

`\begin{gathered} (x+(x-4))*4=216 \\ \Rightarrow(2x-4)*4=216 \end{gathered}`
`\begin{gathered} \Rightarrow8x-16=216 \\ \Rightarrow8x=216+16 \\ \Rightarrow8x=232 \\ \Rightarrow x=(232)/(8)=29 \\ \Rightarrow x=29\text{ km/h} \end{gathered}`

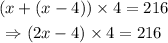
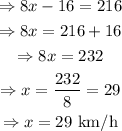
Thus, the faster cyclist is cycling at a rate of 29 km/h (which is the x we have just obtained).

And the slower cyclist is cycling at a rate of (29 - 4) km/h or 25 km/h (which is the (x - 4) we have been writing in the above equation)

Therefore:

Faster cyclist: 29 km/h

Slower cyclist: 25 km/h