We know that the sample n= 37, the mean is 158 and standard deviation is 27. At 95% confidence the interval is given by
![\bar{x}\pm z*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/vabfgmyq2vde9y3azp6pm1cwti40igcta4.png)
where z is equal to 1.96. By substituting the given values into this formula, we get
![158\pm(1.96)\frac{27}{\sqrt[]{37}}](https://img.qammunity.org/2023/formulas/mathematics/college/mzu85cauwx806u862bc801vtmufd5ynqhx.png)
Then, the interval is
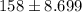
Finally, by rounding up to the nearest tenth, the interval is
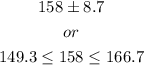
The value for z at 95% confidence is given in the followin table: