ANSWER
See the explanation for the proof.
Step-by-step explanation
First we have to write the secant and the cotangent in terms of sine and cosine:


Replace into the equation,
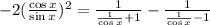
On the left side distribute the square and on the right side do the addition and subtraction in the denominators,
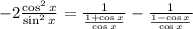
1 over a fraction is equivalent to the reciprocal of the fraction,
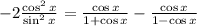
Now do the subtraction on the right side,

Note that the denominator is a difference of two squares,
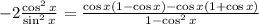
Apply the distributive property on the two terms of the numerator,
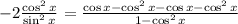
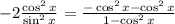
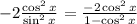
Now, for the denominator remember the trigonometric identity
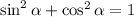
If we solve it for sin²α
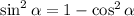
Therefore, the expression we have in the denominator of the right side of the equation is equivalent to sin²x,
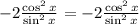
Now we have on both sides,
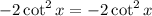
Hence, we have proven that the two expressions are equivalent.