Question

A chemical company makes pure silver by reacting silver nitrate with zinc. The company needs to make 800 grams of pure silver for a client. They have 300 grams of zinc and 600 grams of silver nitrate. Will they be able to make enough silver to fill the order?Zn + 2AgNO3 -> Zn(NO3)2 + 2AgA. No, the zinc nitrate will run out first.B. Yes, they will have exactly enough.C. No, the silver nitrate will run out first.D. Yes, and there will be extra left over.

Answer 1

We will convert the mass of reactants to moles:

`\begin{gathered} moles\text{ }of\text{ }Zn=\frac{mass}{molar\text{ }mass} \\ \\ moles\text{ }of\text{ }Zn=(300.0g)/(65.38gmol^(-1))=4.59\text{ }moles \\ \\ moles\text{ }of\text{ }AgNO_3=(600.0g)/(169.87gmol^(-1))=3.53\text{ }moles \end{gathered}`

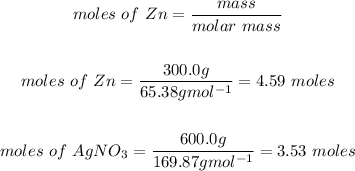
We will now determine the limiting reactant by using the mole to coefficient ratio. The lowest ratio is the limiting reactant:

`\begin{gathered} Zn:(4.59)/(1)=4.59 \\ \\ AgNO_3:(3.53)/(2)=1.77 \end{gathered}`

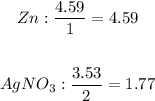
-The silver nitrate has the lowest ratio and is therefore the limiting reactant. The limiting reactant determines how much product can be formed.

We will determine the mass of silver that can be formed from this 600 grams of silver nitrate:

`\begin{gathered} mole\text{ }ratio=2AgNO_3:2Ag=1:1 \\ mass\text{ }Ag=moles* molar\text{ }mass \\ mass\text{ }Ag=3.53mole*107.87gmol^(-1) \\ mass\text{ }Ag=380.78g \end{gathered}`

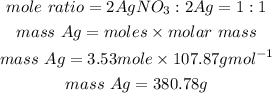
Answer: Based on the calculations we see C) No, the silver nitrate will run out first.