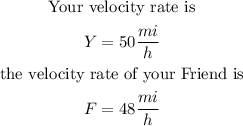Question

You travel 10 min on your bicycle in the same amountof time it takes your friend to travel 8 mi on hisbicycle. If your friend rides his bike 2 mi/h slower than you ride your bike, find the rate at which eachof you is traveling.

Answer 1

Let Y be your velocity rate and F be the velocity rate of your friend. Since your friend rides his bike 2 mi/h slower than you, we can write:

`F=Y-2\ldots(a)`

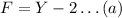
Now, in 10 minutes, your friend travel 8 miles. Then, his velocity rate is

`F=(8mi)/(10\min )`

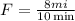
but, in order to use this result, we need to convert miles/minutes into miles/hour. Lets convert it:

`\begin{gathered} (8mi)/(10\min)=(8mi)/(10\min)((60\min )/(1h)) \\ \text{then} \\ (8mi)/(10\min)=48(mi)/(h) \end{gathered}`

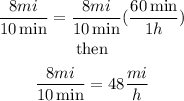
Then, the friend's velocity rate is

`F=48(mi)/(h)\ldots(b)`

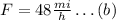
Finally, by substituting this result into equation (a), we have

`\begin{gathered} 48=Y-2 \\ \text{then,} \\ Y=48+2 \\ Y=50(mi)/(h) \end{gathered}`

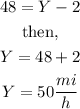
Therefore, the answers are:

`\begin{gathered} \text{Your velocity rate is} \\ Y=50(mi)/(h) \\ \text{the velocity rate of your Friend is} \\ F=48(mi)/(h) \end{gathered}`