Question

Bob Rohrman is offering a 2016 Toyota Camry for $29,000. If you have a $5,000 down payment and are able toborrow the rest at a 2.99% APR on a 48 month loan, how much will your payments be? (round to the hundredthsplaces)

Answer 1

The monthly payments are $513.12

Explanation:

The formula to calculate the monthly payment is:

`P=(r\left(PV\right))/(1-\left(1+r\right)^(-n))`

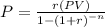
Where:

• P, is the monthly payment

,

• PV, is the present value

,

• r, is the rate per period

,

• n, is the number of periods

After a $5,000 down payment, the present value (PV) would be:

`\begin{gathered} 29000-5000=24000 \\ \rightarrow PV=24000 \end{gathered}`

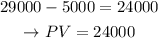
Now, let's transform the APR into the rate per period:

`\begin{gathered} 2.99\%\rightarrow0.0299\rightarrow(0.0299)/(12) \\ \\ \rightarrow r=(0.0299)/(12) \end{gathered}`

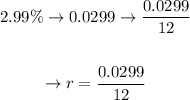
Since the loan is for 48 months, we'll have 48 periods. This way,

`n=48`

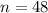
Using all this data in the original formula, we'll get the following:

`\begin{gathered} P=(r(PV))/(1-(1+r)^(-n))\rightarrow P=((0.0299)/(12)(24000))/(1-(1+(0.0299)/(12))^(-48)) \\ \\ \Rightarrow P=513.12 \end{gathered}`

Therefore, we can conlude that the monthly payments are $513.12