Question

The length of a rectangle is six times it’s width. If the area of the rectangle is 150 ft^2, find it’s perimeter. _ft

Answer 1

Let 'L' and 'W' represent the length and width of the rectangle.

Given that the length is six times the width of the rectangle,

`\begin{gathered} L=6\cdot W \\ L=6W \end{gathered}`

The area (A) of a rectangle is given by,

`A=L\cdot W`

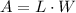
Given that the area is 150 square feet, the expression becomes,

`\begin{gathered} 150=(6W)\cdot W \\ 150=6\cdot W^2 \\ W^2=25 \\ W=5 \end{gathered}`

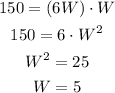
So the width of the rectangle is 5 feet.

The corresponding length will be,

`\begin{gathered} L=6\cdot5 \\ L=30 \end{gathered}`

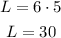
Consider that the perimeter (P) of a rectangle is given by the formula,

`P=2\cdot(L+W)`

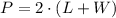
Substitute the values,

`\begin{gathered} P=2\cdot(30+5) \\ P=2\cdot35 \\ P=70 \end{gathered}`

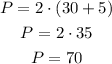
Thus, the perimeter of the given rectangle is 70 feet.