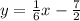Given:
The equation of line c is,
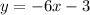
Line d is perpendicular to line c, that means their slopes will be opposite reciprocals.
Slope of line c is,
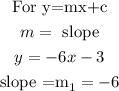
It gives,
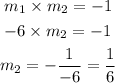
So, slope of the line d is 1/6.
Also line d includes point ( 3, -3 )
The point slope form of equation of line is,
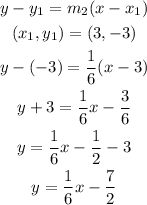
Answer: the equation of line d is,