Given that the number of turns in the primary coil is
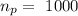
The voltage in the primary coil is
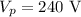
The voltage in the secondary coil is
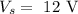
We have to find the number of turns in the secondary coil.
Let the number of turns in the secondary coil be denoted by
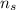
The formula to calculate the number of turns in the secondary coil is
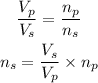
Substituting the values, the number of turns in the secondary coil will be
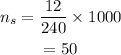
Thus, the number of turns in the secondary coil is 50