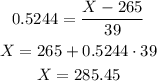Given
Normally distributed
Mean 265 ft
Deviation 39 ft
Procedure
a)
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean and standard deviation, the z- score of a measure X is given by:
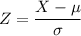
The Z-score measures how many standard deviations the measure is from the mean
b)
X <= 219?
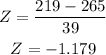
Z-score = -1.17949
P(x<219) = 0.1191
c) Find the 70th percentile
First, we have that the provided z-score is Z=0.5244.