1 Answer

Lukeis · Answer 1 · 2023-02-01T22:58:43+0000

The formula of De Broglie is the following:

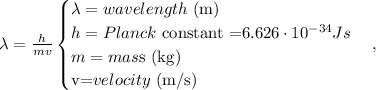
$\lambda=(h)/(mv)\begin{cases}\lambda=wavelength\text{ (m)} \\ h=Planck\text{ constant =6.626}\cdot10^(-34)Js \\ m=mas\text{s (kg)} \\ \text{v=}velocity\text{ (m/s)}\end{cases},$

Remember that the mass of an electron is 9.11 x 10 ^(-31) kg, so replacing in the formula, we're going to obtain:

$\begin{gathered} \lambda=\frac{6.626\cdot10^(-34)J\cdot s}{9.11\cdot10^(-31)\operatorname{kg}\cdot1.48\cdot10^5(m)/(s)}, \\ \lambda=4.91\cdot10^(-9)\text{ m} \end{gathered}$

The answer is that the wavelength of an electron traveling at 1.48 x 10^(5) m/s is 4.91 x 10^(-9) m.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions