Question

I am kinda confused on what to do here Do I have to do - or other things

Answer 1

Given:

(a)

(b)

Find-:

Check for linear, quadratic and exponential.

Explanation-:

Check for linear at the change in x and change of y is same.

(a)

Change of x and y

`\begin{gathered} \Delta x=5-4 \\ \\ =1 \\ \\ \Delta y=48-96 \\ \\ =-48 \end{gathered}`

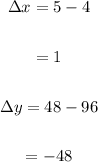
Change of x and y is:

`\begin{gathered} \Delta x=6-5 \\ \\ =1 \\ \\ \Delta y=24-48 \\ \\ =-24 \end{gathered}`

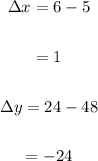
So it is not a linear function

For exponential function: ratio is same for common difference

`\begin{gathered} \text{ ratio}=(96)/(48) \\ \\ =2 \end{gathered}`

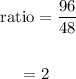
For the second point

`\begin{gathered} \text{ Ratio=}(48)/(24) \\ \\ =2 \end{gathered}`

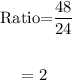
For the third point.

`\begin{gathered} \text{ Ratio }=(24)/(12) \\ \\ =2 \end{gathered}`

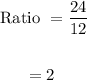
The ratio same so it is an exponential function.

(b)

The change in x and y is:

`\begin{gathered} \Delta x=-2-(-1) \\ \\ =-1 \\ \\ \Delta y=-8-2 \\ \\ =10 \end{gathered}`

Check

`\begin{gathered} \Delta x=-1-(0) \\ \\ =-1 \\ \\ \Delta y=2-8 \\ \\ =-6 \end{gathered}`

So it is not a linear function.

For exponential function.

`\begin{gathered} \text{ Ratio=}(-8)/(2) \\ \\ =-4 \end{gathered}`

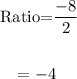
Check for another point,

`\begin{gathered} \text{ Ratio =}(2)/(8) \\ \\ =(1)/(4) \end{gathered}`

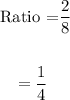
So it is not a exponential function.

Check for quadratic function-:

If the double change of y is same so it is a quadratic function.,

So double difference is -4 for each point so it is a quadratic function.