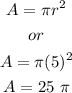Question

The endpoints of a diameter of a circle are A(2,1) and B(8,9). Find the area of the circle in terms of π. A= (Type an integer or decimal. Type an exact answer in terms of π.)

Answer 1

The two points of the circle are A=(2,1) and B=(8,9).

The equation of a circle is

`(x-h)^2+(y-k)^2=r^2`

where (h,k) is the center of the circle and r the radius. We can find the midpoint of these 2 points.

The midpoint is given by

`\text{midpoint}=((x_1+x_2)/(2),(y_1+y_2)/(2))`

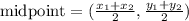
If

`\begin{gathered} A=(x_1,y_1)=(2,1) \\ \text{and} \\ B=(x_2,y_2)=(8,9) \end{gathered}`

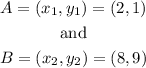
we have

`\begin{gathered} \text{midpoint}=((2+8)/(2),(1+9)/(2)) \\ \text{midpoint}=(5,5) \end{gathered}`

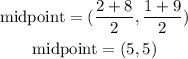
Hence, we have that (h,k)=(5,5). In other words, the equation of the circle is

`(x-5)^2+(y-5)^2=r^2`

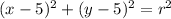
In order to find the area, we must know the radius r. This can be given by substituying one of the given points.

For instance, if we take point (2,1), we have

`(2-5)^2+(1-5)^2=r^2`

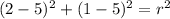
therefore, we obtain that

`\begin{gathered} (-3)^2+(-4)^2=r^2 \\ r^2=9+16 \\ r^2=25 \\ r=\sqrt[]{25} \\ r=5 \end{gathered}`

Finally, the area A of the circle is

`\begin{gathered} A=\pi r^2 \\ or \\ A=\pi(5)^2 \\ A=25\text{ }\pi \end{gathered}`