Question

2. A shop owner raises the price of a $100 pair of shoes by 50%. After a few weeks,because of falling sales, the owner reduces the price of the shoes by 50%. Acustomer then says that the shoes are back at the original price.d. By what percent should the shoes be decreased in order to have the priceback at $100?Kk

Answer 1

d) By 33.3%

Explanations:

Given the original price of the pair of shoe to be $100. If the price increased by 50%, the new price is calculated as:

`\begin{gathered} New\text{ price}=\$100+(0.5*\$100) \\ New\text{ price}=\$100+\$50 \\ New\text{ price}=\$150 \end{gathered}`

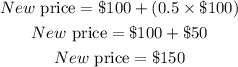
If the price is reduced by 50% due to falling price, the new price of the shoe will be:

`\begin{gathered} New\text{ price}=\$150-(50\%*\$150) \\ New\text{ price}=150-75 \\ New\text{ price}=\$75 \end{gathered}`

This shows that the new price due to falling price is $75

To calculate the percent the shoes be decreased in order to have the price back at $100, we will use the expression below;

`\$100=\$150-(x\%*150)`

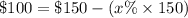
Solve for "x"

`\begin{gathered} 100=150-((150x)/(100)) \\ 100-150=-1.5x \\ -50=-1.5x \\ x=(50)/(1.5) \\ x=33.3 \end{gathered}`

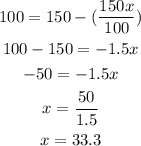
This shows that the shoes should have been decreased by 33.3% to have the price back at $100