Use the formula for the distance between two points to find the lengths MR, RI, IM, BA, AG and GB:
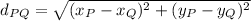
Replacing the coordinates M(-5,5), R(-2,6), I(-2,4), B(2,-2), A(8,0) and G(8,-4) we get:
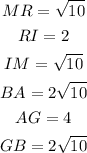
To prove that the triangles MRI and BAG are similar by the SSS similarity theorem, we have to check that the ratio between corresponding parts of the triangles is the same. Notice that:

Since the ratios are the same, then MRI is similar to BAG.
Therefore, the correct choice is the second option: