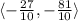Question

Given vector u equals open angled bracket negative 12 comma negative 5 close angled bracket and vector v equals open angled bracket 3 comma 9 close angled bracket comma what is projvu?

Answer 1

- The question would like us to find the projection of u on v given that

`\begin{gathered} u=\langle12,-5\rangle \\ v=\langle3,9\rangle \end{gathered}`

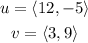
Step-by-step explanation

- The projection of u on v is defined as follows

`\frac{\vec{u}\text{.}\vec{v}}v\mleft\Vert\mright?^2*\vec{v}`

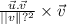
- Thus, we can simply evaluate the projection of u on v using the above definition as follows:

`\begin{gathered} \vec{u}=\langle-12,-5\rangle\text{ can be rewritten as follows:} \\ \vec{u}=-12i-5j \\ \\ \vec{v}=\langle3,9\rangle\text{ can be rewritten as follows:} \\ \vec{v}=3i+9j \\ \\ \text{Thus,} \\ \vec{u}\text{.}\vec{v}=(-12i-5j)(3i+9j) \\ \vec{u}\text{.}\vec{v}=-36i^2-45j^2=-36-45=-81\text{ (Since }i^2=j^2=1) \\ \\ \begin{matrix} \\ \mleft\Vert\vec{v}\mright?\mleft\Vert \mright?^2=(3i+9j)^2=(3i+9j)(3i+9j)=9+81=90\end{matrix} \\ \\ \therefore\text{The projection of u on v is:} \\ \frac{\vec{u}\text{.}\vec{v}}v\mleft\Vert\mright?^2*\vec{v}=-(81)/(90)\langle3,9\rangle=-(9)/(10)\langle3,9\rangle=\langle-(27)/(10),-(81)/(10)\rangle \end{gathered}`

Final Answer

The answer is

`\langle-(27)/(10),-(81)/(10)\rangle`