Question

A regular pentagon has a side length of 2x + 9. A square has a side length of 3x. If both polygons have thesame perimeter, what is a possible solution of x?

Answer 1

The perimeter is the sum of all sides.

The perimeter of the regular pentagon is five times its given expression because it has 5 equal sides.

`P_(penta)=5(2x+9)`

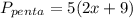
If the square has a side length of 3x, then its perimeter is

`P_(square)=4(3x)`

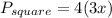
Since both figures have the same perimeter, we express the following equation.

`\begin{gathered} P_(penta)=P_(square) \\ 5(2x+9)=4(3x) \end{gathered}`

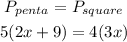
Now, we solve for x.

`\begin{gathered} 10x+45=12x \\ 45=12x-10x \\ 2x=45 \\ x=(45)/(2) \\ x=22.5 \end{gathered}`

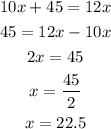
Therefore, the solution of x is 22.5.