Question

Solve the inequality for x and identify the graph of its solution.3|x + 1|<6

Answer 1

Given the inequality::

`3|x+1|<6`

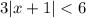
Let's solve the inequality for x and graph.

To solve for x, first divide both sides of the inequality by 3:

`\begin{gathered} (3|x+1|)/(3)<(6)/(3) \\ \\ |x+1|<2 \end{gathered}`

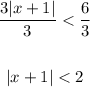
Since the left side is an absolute value, we have two possible solutions:

`\begin{gathered} x+1<2 \\ \\ AND \\ -(x+1)<2 \end{gathered}`

Let's solve each inequality for x:

`\begin{gathered} x+1<2 \\ \text{ Subtract 1 from both sides:} \\ x+1-1<2-1 \\ x<1 \end{gathered}`

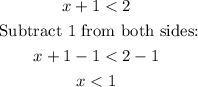
For the second inequality:

`\begin{gathered} -(x+1)<2 \\ -x-1<2 \\ \text{ Add 1 to both sides:} \\ -x-1+1<2+1 \\ -x<3 \\ Divide\text{ both sides by -1:} \\ (-x)/(-1)<(3)/(-1) \\ \\ x>-3 \end{gathered}`

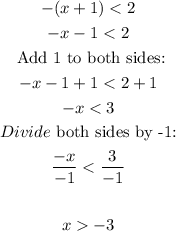
Hence, we have the solutions:

x < 1 and x > -3

Therefore, the solution is:

-3 < x < 1

The graph of the inequality is shown below:

ANSWER:

-3 < x < 1