Given: There are two similar coffee mugs. The white coffee mug can
hold 125 mL, and the blue coffee mug can hold 64 mL. The surface area of the blue mug is 80 cm.
Required: To determine the surface area of the white mug.
Explanation: Let the scaling factors of the similar mugs be (a/b). Then the ratio of the volume of similar mugs will be-
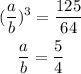
(Note that ratio is a unitless quantity. Hence we don't need to change the unit ml to cubic cm.)
Now the ratio of the surface area is given by-
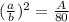
Where A is the surface area of the white mug.
Substituting the value of (a/b) and further solving for A as follows-

Final Answer: The surface area of the white mug is 125 cubic cm.