The initial condition given is that after the first year the person will get 2 vacation days. and each year after that the number of vacation days will double.
So we have:
Number of vacation days Number of years
2 1
4 2
8 3
16 4
until he maxes the vacation days which is 5 workdays = 5 * 5 = 25 (assuming the workweeks are of 5 days) If the workweeks are of 6 days the number will be: 5 * 6 = 30 work days.
So, we need to represent this function :
Number of vacation days (y) in terms of number of years of work (x)
Then we can write:
y = 2^(x) to to the power "x"
which gives: when x = 1 y = 2
when x = 2, y = 4
when x = 3 , y = 8
when x = 4 , y = 16
representing perfectly what we were modeling above based on the problem's description.
So in formal math equation :
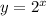
Now we want to find the vacation days he earns after 4 years (which in fact we already calculated to be 16 vacation days. This is the answer for part b.
Now part c asked which year he would have maxed his vacation. So we try to solve for "x" in the exponential equation:
25 = 2^x (or 30 = 2^x if the working days of the week are 6)
to solve for x we need to apply logarithms on both sides (logarithms will bring the exponent "x" down:
ln(25) = x * ln(2)
therefore
x = ln(25) / ln(2)
x is approximately 4.643856...
so it needs more than 4 years, then the top will be reach for year 5 (five)
Let's do now the case for 6 working days per week (since this was not really specified in the problem)
the equation then becomes:
30 = 2^x
ln(30) = x * ln(2)
x = ln(30)/ ln(2)
x approximately 4.9068...
So again, the top will be reached in more than 4, that is 5 years of work
So for both cases we have that after 5 years he has reached his maximum vacation.