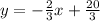Answer:
The slope intercept form of the equation is:
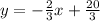
Step-by-step explanation:
Given the equation;
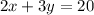
We want to re-write it in slope-intercept form;
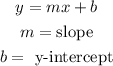
To do that, let us make y the subject of formula in the given equation;
subtract 2x from both sides;
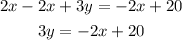
then divide both sides by 3 ( the coefficient of y);
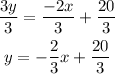
Therefore, the slope intercept form of the equation is;