Question

There are 21 animals on Farmer Colin’s farm – all sheep (s) and chickens (c). If the animals have a total of 56 legs, how many of each type of animal lives on his farm? Write two equations from the given information and solve. Hint: Sheep have 4 legs and chickens have 2 legs.

Answer 1

Given the information stated in the question, we can derive the two following equations:

Step 1: Write out the information in form of mathematical equation.

`\begin{gathered} \text{sheep}=s,\text{ chicken=c} \\ s+c=21 \\ \text{one sheep has 4 legs while one chicken has 2 legs. Hence,} \\ 4s+2c=56 \end{gathered}`

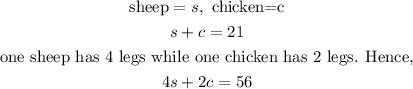
Step 2: We solve the simultaneous linear equations to get the number of sheep and chickens:

`\begin{gathered} s+c=21\Rightarrow equation\text{ 1} \\ 4s+2c=56_{}\Rightarrow equation2 \\ U\sin g\text{ the elimination method, we multiply eq 1 by 2 and eq 2 by 1} \\ 2s+2c=42\Rightarrow eq\text{ 3} \\ 4s+2c=56\Rightarrow eq\text{ 4} \\ eq\text{ 4 minus eq 3} \\ 2s=14 \\ s=(14)/(2)=7 \\ We\text{ have 7 sh}eep \end{gathered}`

Step 3: We get the number of chicken by substituting 7 for s in equation 1:

`\begin{gathered} s+c=21 \\ s=7,\text{ we have;} \\ 7+c=21 \\ c=21-7 \\ c=14 \\ We\text{ have 14 chickens} \end{gathered}`

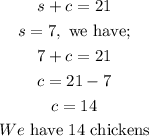
Hence, there are 7 sheep and 14 chickens on Farmer Colin's farm.