(1.1) When we multiply both sides of an inequality by a negative number, the inequality flips oven and instead of "≥" becomes "≤"
(1.2) When we multiply both sides of an inequality by a possitive number, the inequality sign remains unaltered.
(1.3) We need to consider 2 cases because the term (x + 1) could be possitive or negative. If it's possitive the sing remains unaltered, but if (x + 1) < 0, then the sign must change.
(1.4) To solve this, first let's leave 0 in the right hand side of teh inequality:
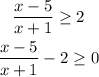
Now add the terms:
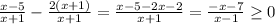
Now we need to calculate the critical points, where the numerator and denominator are 0:
numerator:
-x - 7 = 0
x = -7
Denominator:
x + 1 = 0
x = -1
Now, we have three intervals:
Now we need to test in which intervals teh inequality is true.
For the interval (-∞, -7) Lets take -10:
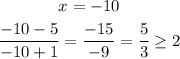
Which is false, 5/3 ≈ 1.666667 which is less than 2.
Next let's test the interval [-7, -1). Let's grab x = -5
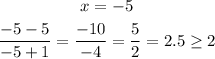
Which is TRUE
Finally, for (-1, ∞) Let's take x = 0:
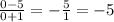
And (-5) is less than 2.
The interval of solutions is:
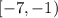
Or:
