Question

4. Given sin 0 = 1/4 and cos 0 ‹ 0, find sec 0.

Answer 1

`\begin{gathered} \text{ Given} \\ \sin\theta=(1)/(4) \\ \cos\theta<0 \end{gathered}`

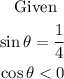
Since the sine function corresponds to the y values, and cosine function corresponds to x value, the quadrant for which x is negative, and y is positive is quadrant II. Knowing this information, we can have the following diagram.

The secant function is the inverse of the cosine function , which means we need to find the adjacent side. Using the Pythagorean Theorem, we have

`\begin{gathered} a^2+b^2=c^2 \\ a^2+1^2=4^2 \\ a^2+1=16 \\ a^2=16-1 \\ a^2=15 \\ √(a^2)=√(15) \\ a=√(15) \end{gathered}`

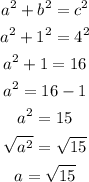
This means that the adjacent side is √15.

Find now sec Θ

`\begin{gathered} \sec\theta=\frac{\text{hypotenuse}}{\text{adjacent}} \\ \sec\theta=(4)/(√(15)) \\ \text{Rationalize the ratio and we get} \\ \sec\theta=(4)/(√(15))\cdot(√(15))/(√(15)) \\ \; \\ \text{Therefore,} \\ \sec\theta=(4√(15))/(15) \end{gathered}`