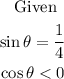
Since the sine function corresponds to the y values, and cosine function corresponds to x value, the quadrant for which x is negative, and y is positive is quadrant II. Knowing this information, we can have the following diagram.
The secant function is the inverse of the cosine function , which means we need to find the adjacent side. Using the Pythagorean Theorem, we have

This means that the adjacent side is √15.
Find now sec Θ
