Step-by-step explanation:
The function is given below as
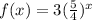
Concept:
An exponential function is a function in which the variable is an exponent. Exponential functions are written in the form f(x)=ab^x f ( x ) = a. b^ x . Initial Value: The initial value of an exponential function is the result of substituting x=0 into the function.
Hence,
by putting x=0, we will have the initial value be
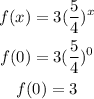
Hence,
The initial value is
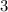
Part B:
The genral equation of an exponential equation is given below as
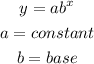
By comparing coefficnets,
The base for this function is
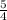
Part C:
The domain of the function is given below as
![\begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<strong>Part D:</strong><p><strong>The range of the function is given below as</strong></p>[tex]\begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)>0\:\\ \:\mathrm{Interval\:Notation:}&\:\left(0,\:\infty \:\right)\end{bmatrix}]()