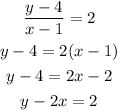Question

Consider the line - 2x - 4y = 3.Find the equation of the line that is perpendicular to this line and passes through the point (1, 4),Find the equation of the line that is parallel to this line and passes through the point (1, 4).Note that the ALEKS graphing calculator may be helpful in checking your answer,

Answer 1

We have the equation of the line;

`-2x-4y=3`

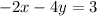
We will rewrite this equation as;

`\begin{gathered} -4y=3+2x \\ \text{divide through by }-4 \\ y=-(3)/(4)-(2)/(4)x \\ y-=-(3)/(4)-(1)/(2)x \end{gathered}`

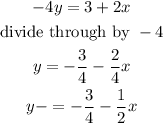
Inspecting this equation, we can see that the slope of this line is;

`-(1)/(2)`

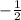
We can now find the equations of the lines needed.

1. A line parallel to the given line and passing through (1,4)

We know that parallel lines have equal slopes, so the slope of this line is still -1/2, lets use the equation of a line fiven slope and a point to obtain the line.

`\begin{gathered} (y-4)/(x-1)=-(1)/(2) \\ 2(y-4)=-(x-1) \\ 2y-8=-x+1 \\ 2y+x=9 \end{gathered}`

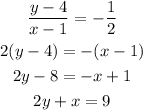
2. A line perpendicular to the given line and passing through (1,4)

The product of the slopes of perpendicular lines is -1, Therefore,the slope of this very line is;

`(-1)/((-(1)/(2)))=2`

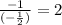
lets use the equation of a line fiven slope and a point to obtain the line.

`\begin{gathered} (y-4)/(x-1)=2 \\ y-4=2(x-1) \\ y-4=2x-2 \\ y-2x=2 \end{gathered}`