Question

Find the minimum value and the maximum value of the function y=3(x - 3)² -4

Answer 1

The minimum value of the function is -8 and the maximum is infinite.

Explanation:

Quadratic function:

In the format:

y = ax² + bx + c

If a is positive, the minimum value is given by:

`y_(MIN)=-(b^2-4ac)/(4a)`

In this question:

First we place in the general format.

y = 3(x - 3)² - 4

y = 3(x² - 6x + 9) - 4

y = 3x² - 18x + 27 - 4

y = 3x² - 18x + 23

So a = 3, b = -18, c = 23

The minimum value is:

`y_(MIN)=-((-18)^2-4\ast3\ast23)/(2\ast3)=-(48)/(6)=-8`

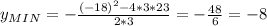
The minimum value of the function is -8 and the maximum is infinite.