Question

Please help me its about systems of equations in three variables2x+4y−5z=18−3x+5y+2z=−27−5x+3y−z=−17

Answer 1

Given the following system:

`\begin{gathered} 2x+4y-5z=18 \\ -3x+5y+2z=-27 \\ -5x+3y-z=-17 \end{gathered}`

notice that we can easily solve for z on the third equation to get the following:

`z=-5x+3y+17`

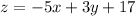
doing the substitution on the first equations we get:

`\begin{gathered} 2x+4y-5(-5x+3y+17)=18 \\ -3x+5y+2(-5x+3y+17)=-27 \\ then\colon \\ 2x+4y+25x-15y-85=18 \\ -3x+5y-10x+6y+34=-27 \\ \Rightarrow27x-11y=18+85=103 \\ -13x+11y=-27-34=-61 \\ \Rightarrow\begin{cases}27x-11y=103 \\ -13x+11y=-61\end{cases} \end{gathered}`

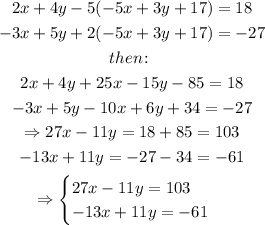
Now, notice that on both equations we get 11y and -11 y, then we can add both of them to find the value of x:

`\begin{gathered} 27x-11y=103 \\ -13x+11y=-61 \\ ----------- \\ 14x=42 \\ \Rightarrow x=(42)/(14)=3 \\ x=3 \end{gathered}`

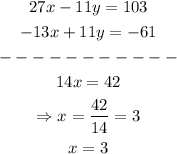
we have that x=3, now we can find y by using this value on one of the previous equations:

`\begin{gathered} x=3 \\ \Rightarrow-13(3)+11y=-61 \\ \Rightarrow11y=-61+39=-22 \\ \Rightarrow y=(-22)/(11)=-2 \\ y=-2 \end{gathered}`

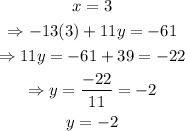
finally, for z we have:

`\begin{gathered} x=3 \\ y=-2 \\ z=-5(3)+3(-2)+17=-15-6+17=-21+17=-4 \\ z=-4 \end{gathered}`

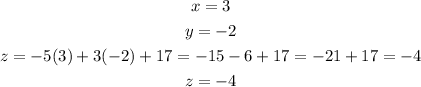
therefore, the solution of the system is (x,y,z)=(3,-2,-4)