Question

Alegrba 2 problems...

Answer 1

38) We must find the value of xx from the following equation:

`\sqrt[]{3\cdot xx-8}=5`

In order to find xx we take the square at both sides:

`\begin{gathered} (\sqrt[]{3\cdot xx-8})^2=5^2 \\ 3\cdot xx-8=25 \end{gathered}`

Now we find the value of x:

`\begin{gathered} 3\cdot xx=25+8 \\ 3\cdot xx^{}=33 \\ x^{}x=(33)/(3) \\ xx=11 \end{gathered}`

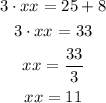
The answer of 38 is: b. 11

33) Again, we must find the value of the unknown xx from the following equation:

`(3)/(xx)=(5)/(xx-2)`

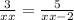
We cross multiply by the denominators and we find:

`3(xx-2)=5\cdot xx`

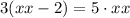
Now we aplly the distributive law for the multiplication:

`\begin{gathered} 3\cdot xx-6=5\cdot xx \\ 3\cdot xx-5\cdot xx-6=0 \\ -2\cdot xx=6 \\ xx=-(6)/(2) \\ xx=-3 \end{gathered}`

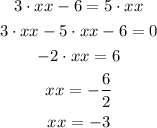
So the answer of 37 is: b. -3