Given,
The initial velocity of the car, u=0 m/s
The final linear velocity of the car, v=28.7 m/s
The time duration, t=8.7 s
The diameter of the tires, d=50.1 cm=0.501 m
The radius of the tires is,
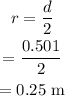
From the equation of motion,
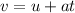
Where a is the acceleration of the car.
On substituting the known values,
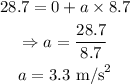
The angular acceleration of the tires is given by,
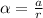
On substituting the known values,
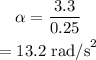
As the initial linear velocity of the car was zero, the initial angular velocity, ω₀ is also zero.
From the equation of motion,
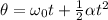
Where θ is the angular displacement of the tire.
On substituting the known values,
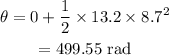
To complete one revolution, the tire has to rotate through 2π radians.
Thus the total number of revolutions made by the tires is,
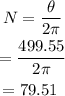
Therefore the total number of revolutions made by the tires is 79.51 which is approximately equal to 79.3202 in the option.