The information given is that 1/10 of her room is painted with 1/2 of a can of paint.
Since 1/10 is equal to 10% and 1/2 is equal to 0.5 of a can:
To paint 10% of her room she needs 0.5 of a can of paint.
Now let's use the previous information to check which of the statements are true:
A. 3 cans of paint will cover 60% of Anne's room
Using our information 10% is covered using 0.5 of a can. We need to multiply by 6 to get 60%, and thus, multiply the number of cans also by 6:
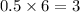
Indeed 3 cans of paint are needed to cover 60% of Anne's room.
Statement A is true.
B. Each can of paint will cover 1/20 of Anne's room.
going back to the initial rate of 1/10 of the room using 1/2 of a can, to find how much is covered by the whole can, we multiply 1/2 by 2, which is a whole can, and also multiply 1/10 by 2:
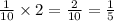
Thus B is not true, because each can of paint will cover 1/5 of the room, not 1/20.
C. Anne's entire room requires 5 cans of paint.
10% requires 0.5 cans. To find the number of cans for the whole room, we need to multiply by 10 to get the 100% (because 10% by 10 gives 100%).
So we also multiply the number of cans by 10:
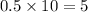
5 cans are needed to paint the entire room.
Statement C is true.
D. Anne's room requires 20 cans of paint.
As we saw in C, the entire room requires 5 cans, not 20. Thus statement D is not true.
E. Painting 1/2 of Anne's room requires 10 cans of paint
Since the entire room requires 5 cans, only 1/2 of the room will require half the cans:
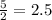
Painting 1/2 of Anne's room requires 2.5 cans, not 10. Thus, statement E is not true.
Answer: