Question

Let n be the number of oil refineries at t years since 2002. A reasonable model of the number of oil refineries is n=-5.12t+139.15 What is the slope? What does it mean in this situation?What is the n intercept? What does it mean in this situation?Predict the number of refineries in 2012

Answer 1

The model given is

`n=5.12t+139.15`

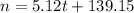
Comparing this with the equation for linear regression

`\begin{gathered} y=bx+a \\ b=\text{slope,a}=\text{ intercept on y} \end{gathered}`

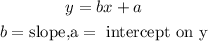
Part A;Hence the slope for the given model is

`-5.12`

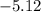
This means the decrease in the number of refineries as the years increases

Part B:The intercept on n is

`\begin{gathered} 139.15 \\ Or \\ (0,139.15) \end{gathered}`

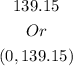
This means the Initial value of the oil refineries at the beginning of the year.

The number of refineries in 2012 will be

`\begin{gathered} \text{between 2002 to 2012 we have 10 years} \\ \text{then t=10} \\ n=-5.12(10)+139.15 \\ n=-51.2+139.15 \\ n=87.95 \end{gathered}`

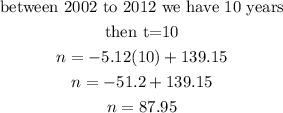
Therefore

the predicted number of refineries is 87.95