Question

Solve the equations below and tell if its is parallel?

Answer 1

The Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In this case you have this equation:

`y-2x=8`

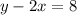
You can write it in Slope-Intercept form by solving for "y":

`y=2x+8`

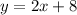
You can identify that:

`\begin{gathered} m=2 \\ b=8 \end{gathered}`

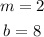
In order to find which equation is parallel to the given line, you need to identify that line whose slope is:

`m=2`

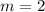
And whose y-intercept is:

`b\\e8`

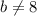
Based on the above, you can determine that this line is the parallel one:

`y=2x+5`

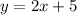
The answer is: Option a.