Question

Drag each function to the box to show the least rate of change and the greatest rate of change

Answer 1

Step-by-step explanation

Given the functions

We can find the function with the least rate of change and the greatest rate of change by finding the slope of the function.

For the first function, we will compare the equation with the general equation of a line which is

`y=mx+c`

Where m is the slope.

By comparison, the slope of the first equation would be 5.

For the second function, which is denoted by a table of values, we will find the slope by picking two points from the table and inserting it into the slope formula below.

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ where\text{ }x_1=0,y_1=-3\text{ }and\text{ }x_2=2\text{ and }y_2=3 \\ \end{gathered}`

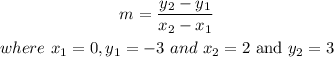
Therefore, we will have;

`m=(3-(-3))/(2-0)=(6)/(2)=3`

Hence, the slope of the second function is 3.

Therefore, the answer is