Question

Consider △ABC, where a = 7, c = 10, and m∠C=38∘.What are the measures of the missing angles and missing side?

Answer 1

• A=25.5°

,

• B=116.5°

,

• b=14.5 units

Explanation:

Given triangle ABC where:

• a = 7

,

• c = 10

,

• m∠C=38°

(a)First, we find the measure of angle A using the law of sines.

`(\sin A)/(a)=(\sin C)/(c)`

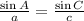
Substitute the given values:

(b)Next, we find the measure of angle B.

The sum of the measures of angles in a triangle is 180 degrees.

`\begin{gathered} 38\degree+25.5\degree+m\angle B=180\degree \\ m\angle B=180\degree-(38\degree+25.5\degree) \\ m\angle B=116.5\degree \end{gathered}`

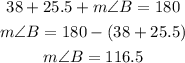
The measure of angle B is 116.5 degrees.

(c)Finally, we find the length of b.

`(b)/(\sin B)=(c)/(\sin C)`

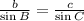
Substitute the given values:

`\begin{gathered} b=(c)/(\sin C)*\sin B \\ =(10)/(\sin38\degree)*\sin116.5\degree \\ =14.5 \end{gathered}`

The length b is 14.5 units.