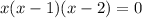Question

Write an equation that has three solutions,0,1, and 2

Answer 1

A polynomial with a n degree has n solutions. The degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients.

A third degree polynomial has 3 solutions. A third degree polynomial, has the following form

`P(x)=ax^3+bx^2+cx+d`

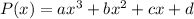
If the third degree polynomial has 3 distinct roots, it can also be written in factorized form, which is

`ax^3+bx^2+cx+d=a(x-x_1)(x-x_2)(x-x_3)`

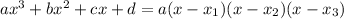
To find the roots, we just have to find the solutions for the polynomial when it is equal to zero.

`a(x-x_1)(x-x_2)(x-x_3)=0`

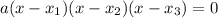
If we use 0, 1 and 2 as the solutions for this equation, we have

`\begin{gathered} a(x-0_{})(x-1)(x-2)=0 \\ x(x-1)(x-2)=0 \end{gathered}`

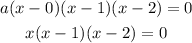
This is an equation with three solutions, and they are 0, 1 and 2.

`x(x-1)(x-2)=0`