SOLUTIONS
For the polynomial P(x) = 4x^2 + 7x + 8 and c = 1
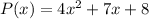
where c = 1
(a) By direct substitution
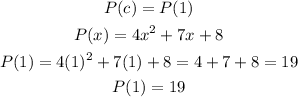
(b) The Remainder Theorem states that when we divide a polynomial
P(x) by x - c the remainder R equals P(c)

From the remainder theorem , the remainder = 19