Question

Using factoring, what are the solutions to the polynomial below? 2x ^ 3 + 4x ^ 2 - 30x = 0

Answer 1

We can start solving the solution to the polynomial given by factoring out 2x, getting:

`2x(x^2+2x-15)=0`

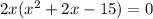
The expression inside the parenthesis is a quadratic equation. By methods of factoring, we can rewrite this as:

`\begin{gathered} 2x((x+5)(x-3))=0 \\ 2x(x+5)(x-3)=0 \end{gathered}`

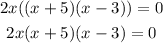
Solving for the value of x that satisfies the polynomial given, we have:

`\begin{gathered} 2x=0,x+5=0,x-3=0 \\ x=0,x=-5,x=3 \end{gathered}`

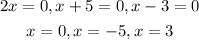
Hence, the solutions to the polynomial given are x = -5, 0, 3.

Answer: x = -5, 0, 3