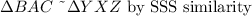Answer:
The triangles are similar.
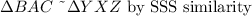
Step-by-step explanation:
Given the triangles in the attached image;
we want to confirm if they are similar.
Let us compare the ratio of corresponding sides of the triangles.
For them to be similar the ratio of the corresponding sides of the triangles must be equal.
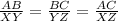
substituting the values in the figure;
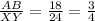
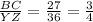
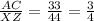
The ratio of the corresponding sides are equal.
Therefore, the triangles are similar.