Answer:
• BC = 7√5 units.
,
• m∠B=41.8°
,
• m∠C=48.2°
Explanation:
First, find the length of the third side, BC using the Pythagorean theorem.
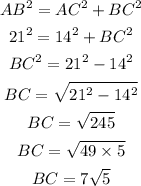
The length of the third side, BC is 7√5 units.
(b)Next, find the measure of angle B.
• The side length ,opposite, B = 14
,
• The length of the ,hypotenuse, = 21
From trigonometric ratios:
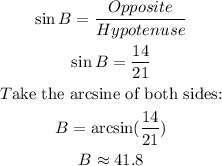
The measure of angle B is 41.8 degrees.
(c)Finally, find the measure of angle C.
In a right triangle, the sum of the two acute angles is 90 degrees, therefore:
![\begin{gathered} m\angle B+m\angle C=90\degree \\ 41.8\operatorname{\degree}+m\operatorname{\angle}C=90\operatorname{\degree} \\ m\operatorname{\angle}C=90\operatorname{\degree}-41.8\operatorname{\degree} \\ m\operatorname{\angle}C=48.2\operatorname{\degree} \end{gathered}]()
The measure of angle C is 48.2 degrees.