We know that the piano loses 20% of its value each year, this means $4,000 is 80% of %5,000, $3,200 is 80% of $4,000.
For year 3, we have
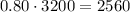
For year 4, we have
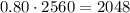
Hence, option D is correct.
Let's find the value after 16 years. We know that the ratio of the sequence is 0.80 and the first term is 5,000, let's use the formula for geometric sequences.
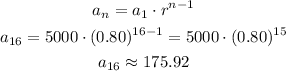
Hence, after 16 years, the value would be $175.92, approximately.