Question

Number 10 Find the limit Use the x values: -0.03, -0.02, -0.01, 0, 0.01, 0.02, 0.03

Answer 1

Question 10:

In this case we have to calculate the limit of the function when x approaches 0.

As the function is defined piecewise and the point where the definition of the functions changes is at x=0.

Then, we will have a definition for the function when we approach x=0 from the right or from the left. For the limit to exist, both limits (from the right and from the left) should have the same value.

We use the function that is defined for x≤0 to calculate the value of the limit approaching from the left:

`\lim _(x\to0^-)x^2+4x+4=0+0+4=4`

Then, we use the function defined for x>0 to calculate the limit approaching from the right:

`\lim _(x\to0^+)4e^(4x)+\ln (x+1)=4e^(4\cdot0)+\ln (0+1)=4\cdot e^0+\ln (1)=4+0=4`

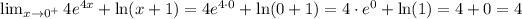
Then, as both limits have the same value, the limit exist and has a value of 4:

`\lim _(x\to0)f(x)=\lim _(x\to0^-)f(x)=\lim _(x\to0^+)f(x)=4`

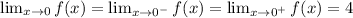
Using values for x

In this case, we calculate the limit using values for x approaching the value of the limit (x=0).

As we have two different functions for x≤0 and x>0, we use the corresponding function for each of the values.

For negative values and zero, we use this function:

`f(-0.03)=(-0.03)^2+4(-0.03)+4=0.0009-0.12+4=3.8809`
`f(-0.02)=(-0.02)^2+4(-0.02)+4=0.0004-0.08+4=3.9204`
`f(-0.01)=(-0.01)^2+4(-0.01)+4=0.0001-0.04+4=3.9601`
`f(0)=(0)^2+4(0)+4=0-0+4=4`

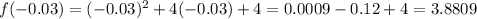
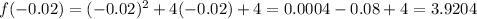
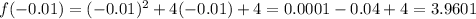
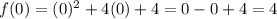
For the positive values, we use the other function:

`f(0.03)=4e^(4\cdot0.03)+\ln (0.03+1)=4e^(0.12)+\ln (1.03)\approx4.5100+0.0295\approx4.5395`
`f(0.02)=4e^(4\cdot0.02)+\ln (0.02+1)=4e^(0.08)+\ln (1.02)\approx4.3331+0.0198\approx4.3529`

`f(0.01)=4e^(4\cdot0.01)+\ln (0.01+1)=4\cdot e^(0.04)+\ln (1.01)\approx4.1632+0.0099\approx4.1731`

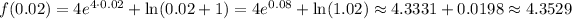
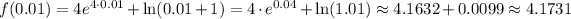
We can see that, as we did before with the calculation of the limit, approaching from both sides of x=0 give the same result. That is one of the conditions for the limit to exist: to give the same value approaching from both sides.

Answer: 10) the value of the limit is 4.