Question

Amy can clean the house in 7 hours. When she works together with Tom, the job takes 5 hours. How long would it take Tom, working by himself, to clean the house?

Answer 1

Given:

a.) Amy can clean the house in 7 hours.

b.) When she works together with Tom, the job takes 5 hours.

Let,

T = no. of hours Tom can clean the house

In this type of problem, we will be using the following formula:

`\text{ }(1)/(t_1)\text{ + }(1)/(t_2)\text{ = }(1)/(t_b)`

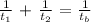
Where,

1/t1 = time taken by first person

1/t2 = time taken by second person

1/tb = time taken if both do the work together

We get,

`\text{ }(1)/(7)\text{ + }\frac{1}{\text{ T}}\text{ = }(1)/(5)`
`\frac{\text{ T + 7}}{\text{7T}}\text{ = }\frac{1}{\text{5}}`
`\text{ 5\lparen T + 7\rparen = \lparen1\rparen\lparen7T\rparen}`
`\text{ 5T + 35 = 7T}`
`\text{ 5T - 7T = -35}`
`\text{ -2T = -35}`
`\text{ }\frac{-\text{2T}}{-2}\text{ = }(-35)/(-2)`
`\text{ T = 17.5 Hours}`

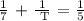
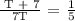
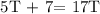
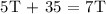
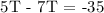
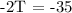
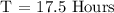
Therefore, Tom could finish cleaning the house in 17.5 Hours

The answer is 17.5 Hours