Give:
There are give that the principle amout is $1000.
Step-by-step explanation:
Accordig to the question:
We need to find the actual amount.
So,
From the formula of compound interest quarterly.
![A=P[1+((r)/(4))^(4t)]-P](https://img.qammunity.org/2023/formulas/mathematics/college/pdqccmxfwkwx5yov5fhn12fhsax8i9o0fz.png)
Where,
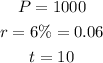
Then,
Put all the above values into the given formula:
So,
![\begin{gathered} A=P[1+((r)/(4))^(4t)]-P \\ A=1000[1+((0.06)/(4))^(4(10))]-1000 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pbg35s1iwde8xrh2uvwh9559srui71usa1.png)
Then,
![\begin{gathered} A=1000[1+((0.06)/(4))^(4(10))]-1000 \\ A=1000[1+((0.06)/(4))^(40)]-1000 \\ A=1000[1+(0.015)^(40)]-1000 \\ A=1814.02-100 \\ A=814.02 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k0qj0u2na7oawx97nnyfdgn87wsvud5cz3.png)
Final answer:
Hence, the amount is $814.02.