Given,
The time it takes for the wave to travel between two docks, t=5.2 s
The distance between two docks, d=19 m
The wavelength of the wave, λ=1.5 m
The speed of the water wave is given by,
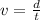
On substituting the known values,
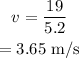
The relation between the speed of the water wave and the frequency is given by,
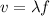
Where f is the frequency of the water wave.
On substituting the known values,
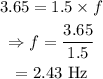
Thus the frequency of the water wave is 2.43 Hz